Journal of Civil, Structural and Transportation Engineering (JCSTE)

1. Introduction

Balanced cantilever method being generally used for long span concrete bridges over 80 m in the cases where the other technology cannot to be used due to inaccessible terrain or other similar problems. Cast in-situ segments are realized by the step by step method and each segment has a different age and different property of concrete respectively. Rheological effects in concrete as a differential shrinkage, creep and thermal effects have a significant impact on a stress distribution along the cross-section and along the span. Particularly in cases where the structural scheme has been changed over the time. Deformation behaviour and stress level of the structure in service depends on accurate long-term effect prediction. Structural design or reliability assessment of long span bridges need to adopt a range of input assumptions due to the entire structural behaviour within the construction stages especially the load history. In these cases the long-term monitoring has a great significance. It can enable to work with the actual stress level along the span and also the cross-sections over a determined time. Two important outputs of the bridge monitoring can be defined. The first one concerns to the bridge design feedback and suitable structural modelling from the stress and deformation prediction point of view. The second one concerns to the fact that it enable to perform the bridge analysis based on the actual stress distribution in structure. If it is required by technical condition to carry out the structural analysis of that bridge in the future bridge administrator will have all relevant information to do that.

Therefore one representative of such long span bridge constructed by the balanced cantilever method in Slovakia on the highway D1 has been chosen. This is bridge No. 205 that was recently built (in 2014) in northern part of Slovakia, near the city Zilina. University of Zilina and the contractor company Vahostav-Sk, have been cooperated on that research work. Whole experimental program has been proposed in order to obtain the real structural behaviour of the bridge over the time from the construction stages to the service. In-situ recorded data acquired from our proposed monitoring program have been compared with the theoretical one. They were derived from the well-known prediction theories based on the Eurocode 2 rheological models, [4], [5] and the Model Code 2010, [6] too. It was applied to the numerical time dependent FEM models.

2. Bridge and Monitoring System Description

Prestressed concrete bridge No. 205 has five spans (75.0 m + 120.0 m + 75.0 m + 53.0 m + 37.0 m), with total length of 362.0 m. The main span (120.0 m) bridging the river Vah had been cast by the balanced cantilever method and other spans by the permanent scaffolding method, see Figure 1. Length of each cantilever is 49.0 m and consists of 11 segments with length of 5.0 m. The cross-section is a typical single cell box girder. Width of the top slab is 13.65 m and the bottom slab is 7.0 m. The cross-section depth is variable, from 2.85 m in the middle of span to 6.5 m above the support. Thickness of the webs varies from 450 mm (middle of span) to 800 mm (above the supports). The top slab has a constant thickness 300 mm, the bottom slab varies from 240 mm (middle of span) to 920 mm (above the supports).

The concrete strength class has been designed C40/50 and prestressing tendons with characteristic strength of 1860 MPa. The tendons consist of 15 or 18 strands with diameter of 15.7 mm.

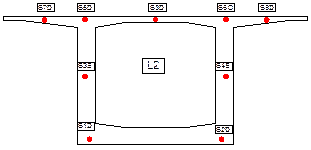
The type TES/5.5/T embedment vibrating wire strain gauges for concrete in the decisive cross-sections in the first segment (L1) and (L2) near the supports of the cantilever and in the middle closure (UL) have been installed, see Figure 2.

There were monitored the strains and temperature in certain fibres of concrete cross-sections continually. Concreting traveller started casting of the first (V1) cantilever. There was time difference around 140 days between the cantilever V1 and V2 erecting. Both of the cantilevers joining have occurred after 380 days.

3. Structural Model of the Bridge

The numerical analysis of the bridge was performed in the MIDAS Civil system with the basic concrete creep and shrinkage prediction models according to the Eurocode 2 standard especially STN EN 1992-1-1, [4] and STN EN 1992-2, [5]. Own prediction model have been based on acquired concrete parameters from experimental tests in the laboratory. Bearing structure was modelled using linear beam 1D elements as a time dependent analysis using the time step by step method and real load history considering, see Figure 3.

The concrete shrinkage along the cross-section was modelled using uniform function as the first approach. The second one more accurate model was based on the differential shrinkage principle. The cross-section of each segment was divided into three parts according to the real time steps, see Figure 3. For that reason the time dependent effects were acting exactly by course of each construction stage according to above mentioned standard approaches and real measured parameters. The recorded temperatures in each parts of cross-section, was applied as a nonlinear temperature gradient, see Figure 4. 2D model for simulation of that problem had also been prepared, as for example at Halvonik et al., [2].

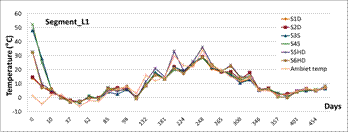
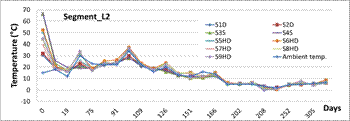
Within the first segment (L1) casting the highest temperature of concrete was observed in the web, smaller in the top slab and the lowest in the bottom slab due to the fact that this part of cross-section was casted earlier about 5 days than the other ones. After several days the temperature of both of slabs became approximately unified, see Figure 4. But the temperature of the webs remained significantly higher for longer time. But over the time the elevated temperatures produced by the hydration process in concrete became declined and slabs and webs were affected only by the ambient temperatures and gradually unified. Very different climatic conditions were recorded within both of cantilever concreting. The first one (L1) was cast over the winter condition with temperature ranging by (-6 ≈ +11^oC) and the second one (L2) during the summer time (+15 ≈ +28^oC). Relative humidity reached the different values also on the (L1) it was around 70-90% and on the (L2) between 40-60%.

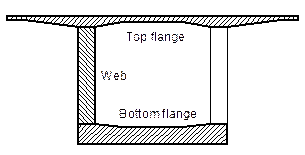
The concrete age of each member were measured from the actual time schedule of concrete casting and prestressing. Each segment had an appropriate compressive strength and modulus of elasticity at construction stage depending on the verified values in laboratory.

The general incremental step-by-step method was applied for the analysis. For the stress analysis of such non-homogenous structures where the basic concrete properties and the structural scheme were varying on the structure within the time (e.g. cantilever construction method) is particularly recommended Annex KK.101, of the Eurocode 2 approach, [5]. The fundamental equation for time dependent concrete strains is

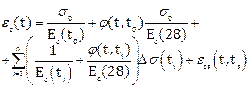
In this equation the first term represents the instantaneous deformations due to a stress applied at t_o. The second term represents the creep due to this stress. The third term represents the sum of the instantaneous and creep deformations due to the variation in stresses occurring at instant t_i. The fourth term represents the shrinkage deformation.

4. Some Results of the Bridge Monitoring

Experimental research program was divided to the laboratory testing and continual in-situ bridge monitoring over the time. As the main purpose of the laboratory tests were acquiring the real values of the concrete basic mechanical properties and to verify the time development magnitude of time dependant strains due to the concrete creep and shrinkage effects. They were later used as an input data for the theoretical model.

4. 1. Laboratory Test Results

We have prepared 3 concrete specimens for each part of cross-section (evaluated on the cube shape of specimen) within the each monitored segment casting to get an actual value of concrete strength. And 3 concrete specimens (prism shape) for the evaluation of the modulus of elasticity, see Figure 5.

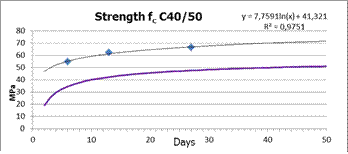
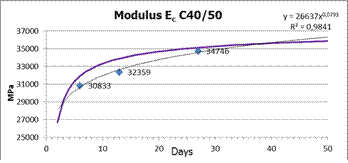
The basic mechanical parameters of concrete were gained for the 7, 14 and 28 days age of concrete. Strain gauges were applied for the strain recoding. The long-term concrete strains development over the time due to the creep and shrinkage effects was continuously investigated on the 9 prism specimens. The theoretical curves based on the concrete creep and shrinkage prediction model according to the STN EN 1992-1-1, [4], STN EN 1992-2, [5], Model Code 2010, [6] and the Model B3 have been compared with the recorded values of strains, see Figure 6.

4. 2. Some Results of the Bridge In-situ Monitoring

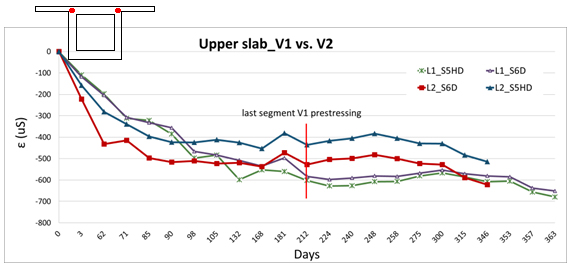
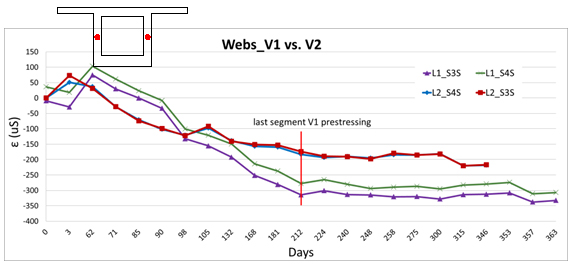
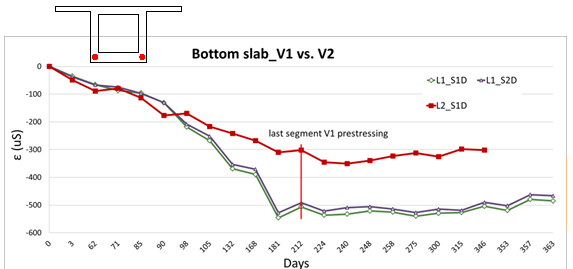
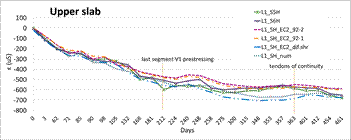
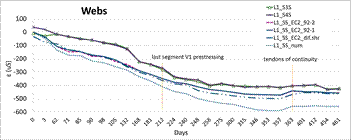
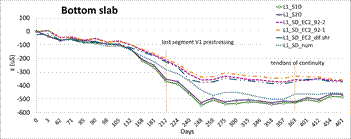
The long-term strains in concrete in characteristic cross-sections of the bridge are presented at the following graphs, see Figure 7, where labelling T - that means strain gauge, L or P - that means left side or right side of the prism specimen and 1 or 2 - that means number of specimen. Only the selected strains in top and bottom fibres and in the web ones have been presented.

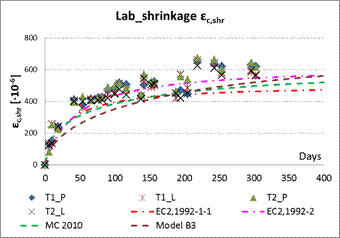
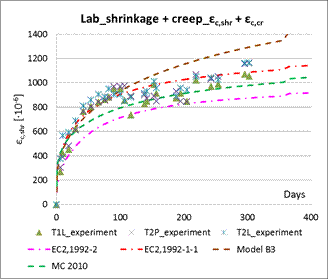
Quite good coincidence between the monitored values of the strains in slabs and webs of the cross-section has been achieved, see Figure 7. But noticeable deviations mainly between strains in webs and bottom slab being demonstrate the effects of concrete non-homogeneity from the various temperature and humidity influences point of view. More massive parts of the cross-section are more sensitive to above mentioned effects. Thinner upper slab showed quite similar courses of strains on both of cantilevers.

Time dependent analysis was applied for phased structural 1D model with the stress redistribution along the structure and along the cross section (3 parts) due to different time of cross-section concreting. The influences of actual temperature and humidity in the concrete still remain the problem how it takes into account in the practical analysis using a 1D numerical model. Some results of the strains courses are presented in Figure 8.

Quite good agreement between the real monitored values and the theoretical ones on the top and bottom slab of the cross-section were achieved, see Figure 8. Two approaches of concrete creep and shrinkage prediction provided by Eurocode 2 and model based on measured concrete parameters had been used. In the case of strains in the web the 2D model had to be used again due to appropriate temperature effects and the shear deformation of web simulation. That is caused by the tensile stresses in the webs at the early stages, see Figure 7. That effect being significant in the case of short cantilever phases that means the dimension of cross-section depth is relatively the same as in the longitudinal direction.

5. Conclusion

Presented results are shown the possibility to record and analyze the long-term effects on complicated cast-in-place non-homogenous bridge structure that is characterized by the significant load history and the structural change over the time. Combination of methods of the continual monitoring system, laboratory experiments with the appropriate numerical modeling appears to be a good way to get the more accurate pictures about the real structural behaviour in time. Quite good agreement between in-situ recorded strains in the characteristic fibers of cross-section and the theoretical ones based on the rheological prediction models provided by Eurocode 2 and our parametric model were shown. In standard numerical model the shrinkage effect on the concrete box girder bridges has been usually assumed as the strains linearly distributed over the cross-section. But actual structural behaviour is more complicated. Effect of differential cross-section shrinkage causes the stress distribution also in the longitudinal direction in such non-homogenous structure. Taking into account this fact the time dependent model with divided cross-section much better reflects the reality. The underestimation the load history and differential shrinkage effect can lead to the wrong assumptions for the future prediction of deformation and redistribution of the stresses in the structure. Temperature and relative humidity are important environmental factors which are affecting to the axial stresses distribution. Nonlinear temperature distribution along the cross-section depth is very complicated problem for the 1D model. In that cases the 2D models can be successfully applied.

In spite of the problems including a lot of environmental and structural influences our current experiences based on comparison of monitored bridge behaviour with the theoretical approaches can offer the new bridge design feedback and better understanding the non-homogenous structures behaviour generally. Long-term monitoring and analysis of current modern concrete structures has remarkable significance from having knowledge about stresses distribution stage point of view. It can enable to perform future more accurate structural analysis of bridges in service, as shown for example by Vican et al., [3].

Acknowledgements

This presented research work has been supported by the Slovak Grant Agency VEGA, No. 1/0336/15 and No. 2/0033/15 and the Slovak Grant Agency APVV, No. APVV-0106-11 and No. APVV -0736-12 and supported by European regional development fund and Slovak state budget by the project "Research Centre of University of Zilina", ITMS 26220220183.

References